Homework 4 - Problem 3

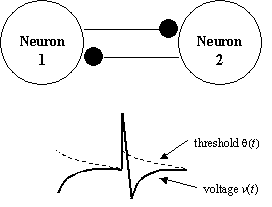
3. In this problem you will construct a two-neuron oscillator using reciprocal inhibition. The neurons will be modeled as leaky integrate-and-fire units with an adaptive threshold mechanism that generates firing-rate adaptation and post-inhibitory rebound.  The model structure is illustrated in the following diagram: The update equations for each individual neuron are: Remember that the input u(t) comes from spike activity of the presynaptic unit. The parameter values for the model are: Both neurons should receive constant current injection. To break the symmetry of the model, inject slightly more current into neuron 1 than neuron 2.  Specifically, inject 1.1 nA into neuron 1 and 0.9 nA into neuron 2. When the neuron fires an action potential, reset the membrane voltage to Einh on the next time step (rather than 0, as was done in HW 2).  [Note: This is related to the adaptive threshold level, which can fall below zero in this model, but not below Einh. 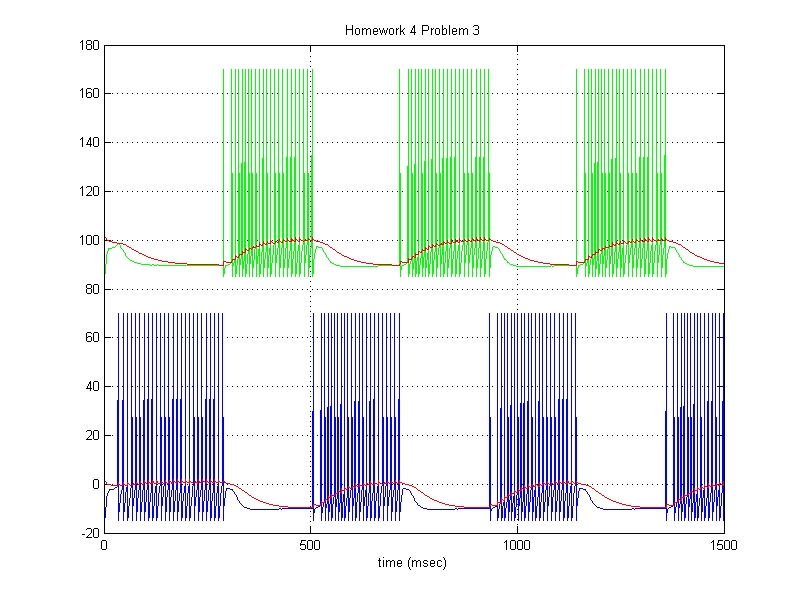We need to reset the membrane voltage to a value that is below the threshold level, hence we choose Einh as the reset value.] The output of your simulation should look similar to the following graph (BLUE: neuron 1, GREEN: neuron 2, RED: threshold level):

HOMEWORK home page