Neuro 317 Methods in Computational Neurobiology
Univ. of Illinois, Urbana-Champaign
Prof. Mark Nelson

Homework 3 - Problem 2

2. Now we're going to simulate the response of the squid giant axon to a step current injection. The HH model for the squid giant axon is described by the following set of equations:

 

 

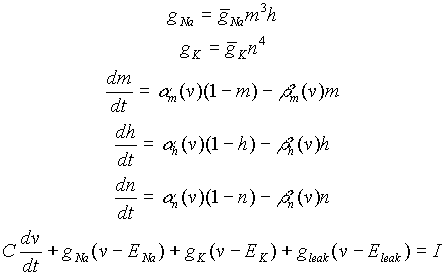
with the following parameter values:

 

 

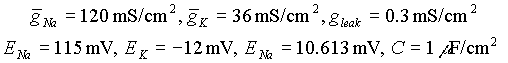
Use the six subroutines from HW #3.1 above when evaluating the rate constants. Initialize the HH state variables at v=Vrest before starting the main simulation loop. Use Euler integration with an integration time step of 0.025 msec (Note: deltaT is a factor of 40 smaller than we used in our integrate-and-fire simulations in HW #2. This is necessary for numerical stability - more on this topic in the next homework assignment.) The structure of your simulation code should be something like the following:

 

initialize parameter values.

initialize v to Vrest.

initialize m, n, & h to their steady-state values at Vrest.

LOOP:

compute injection current for this time step.

get values of v, m, n, & h from previous time step.

use these values to compute gNa, gK, dm/dt, dn/dt,

dh/dt, and dv/dt according to the ODEs given above.

update m, n, h, and v using the Euler method.

END LOOP

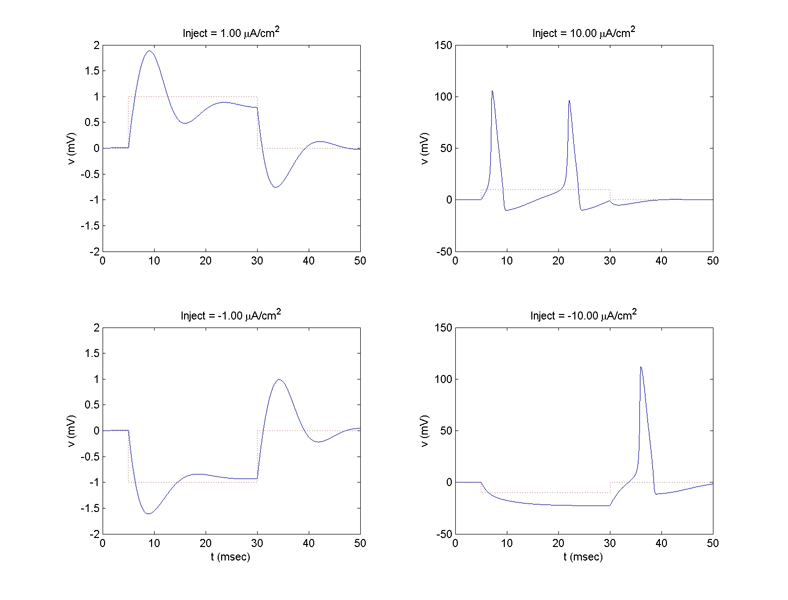
generate plots
 

   (a) Simulate the subthreshold response of the axon to weak depolarizing (I = +1.0 µA/cm2) and hyperpolarizing (I = -1.0 µA/cm2) current pulses. Use a 25 msec pulse duration (5 < t <= 30), and simulate 50 msec of the response (0 < t <= 50).

 

(b) Now simulate the response to strong depolarizing (I = +10.0 µA/cm2) and hyperpolarizing (I = -10.0 µA/cm2) current pulses. Use a 25 msec pulse duration (5 < t <= 30), and simulate 50 msec of the response (0 < t <= 50). What do you think causes the action potential at the end of the hyperpolarizing pulse?

Turn in your MATLAB code and response plots.

 

 Your output should look similar to the following plots. Note the difference in vertical scale between the left-side and right-side plots.

VIEW SOLUTION

<- HOMEWORK home page