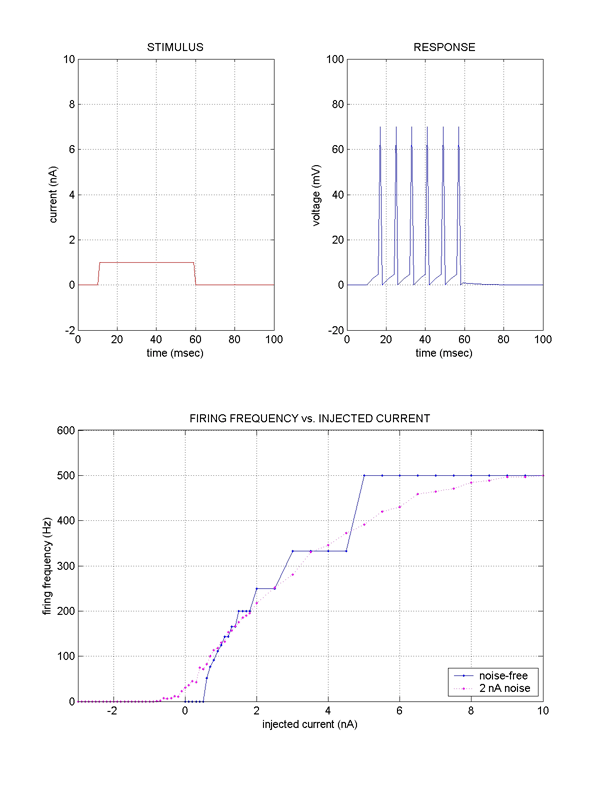

In this model, the minimum current injection level for spike generation
is 0.5 nA.
This value can be calculated by recalling that for constant current
injection I, the steady-state voltage V_ss of the RC circuit is I*R.
Spike generation occurs when V_ss >= V_thr, thus the threshold current
is
I_thr = V_thr/R = (5 mV)/(10 MOhm) = 0.5 nA.
Why does the firing rate saturate for large currents?
In the model, the maximum firing rate is determined by the minimum number of integration time steps required to generate a spike, reset the voltage to zero following the spike, and prepare to generate the next spike. In this particular implementation, the minimal cycle time is two time steps (one to integrate & fire, one to reset). With an integration time step of 1 msec this implies that the minimum interval between spikes is 2 msec -- thus the maximal firing rate is 1/(.002 sec) = 500 Hz. If one changed the integration time step DT to a different value in this model, the maximal firing rate would also change. One enhancement to this simple integrate-and-fire model would be to add an explicit refractory period to limit the peak firing rate to a predetermined value (e.g., an absolute refractory period of 10 msec would limit the maximum firing rate to 100 Hz.)
 HOMEWORK home page
HOMEWORK home page