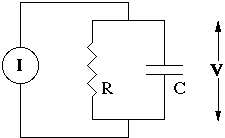
Write down a differential equation that describes the behavior of the RC circuit shown below. The equation should describe the voltage change (dV/dt) as a function of the applied current (I). Arrange the equation such that the term (dV/dt) is alone on the left-hand side of the equation and all of the other terms are on the right.
Solution:
Define i_R as the current through the resistor,
i_C as the current through the capacitor,
I as the total current, and V as the voltage drop.
| Current conservation dictates: | I = i_R + i_C | (1.1) |
|---|---|---|
| The resistive current is give by Ohm's law: | I_R = V/R | (1.2) |
| The capacitive current is give by: | i_C = C (dV/dt) | (1.3) |
| Substituting (1.2)-(1.3) into (1.1) | I = (V/R) + C (dV/dt) | (1.4) |
| Rearranging (1.4) to solve for dV/dt: | dV/dt = -V/(RC) + I/C | (1.5) |
| dV/dt = -V/(RC) + I/C |
|---|
HOMEWORK home page