
Medicinal leech, Hirudo medicinalis

Medicinal leech, Hirudo medicinalis
Scientific interest in leeches date back to ancient India. However, the first Western citation is credited to the Greek, Nicander of Colophon (c 130 BC). These early references were accounts of the use of leeches for bloodletting. This therapeutic use of leeches, the medicinal leech in particular, reached a height between 1825 and 1840. A more contemporary use of leeches was dicovered in 1957 by Markwardt. The leech secretion hirudin was isolated and subsequently its anticoagulant properties with respect to the elucidation of blood clotting mechanisms were examined.
Today medicinal leeches are used as tools in tissue grafts and reattachment surgery. Not only do they secrete anitcoagulants to prevent blood clots and relieve pressure due to pooling blood. It appears that leech saliva has other therapeutic properties. Leech saliva helps reestablish blood flow to reattached body parts by means of a vasodilator, provides a numbing anesthetic, and lessens the risk of infection due to an antibiotic.
Although leech feeding may be the first behavior one associates with medicinal leeches, neuroethologists have examined this species with particular interest in interneuronal oscillators. The advantage of this preparation stem from the simplicity of its central nervous system (CNS).
Tree of Life: Hirudinae
Leech swimming is produced by an anterior to posterior traveling wave of body undulation. The progressive movement of peaks and troughs along the aminal's body is called a metachronal wave (see figure below) whose cycle period varies according to swimming speed (350 to 2000ms.). Interestingly, a single wavelength is generated at all swim speeds (cycle periods). It appears that a single wave in the body represents a compromise between thrust efficiency and stability. A larger thrust could be generated with the body shaped into a half-wave, however, this waveform would lead to pitching of the head. Thus, intersegmental delays in body movement vary with cycle period to maintain constant intersegmental phase lags near 20 degrees. Although sensory feedback from body wall movements help establish intersegmental phase lags. Mechanical properties of the hydroskeleton and the hydrodynamics of the body provide the primary contribution to these motor phase lags. These swimming movements are the result of a central oscillator network.
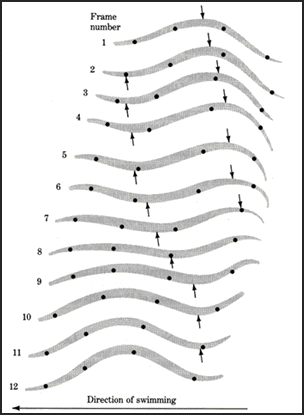
Leech swimming. Arrows indicate posteriorly propagating peak and trough.
Picture from Camhi (1984).
The medicinal leech CNS is composed of 34 ganglia. The head ganglion consists of six fused ganglia while seven ganglia form the tail ganglion. Between the head and tail (leech length varies from five to 10cm) is the segmental nerve cord which consists of the remaining 21 ganglia. Each segmental ganglia contain approximately 200 pairs of neurons with cell bodies ranging from 10 to 100 microns in diameter. Over 50 of these pairs of neurons have been identified and it is known that a pair of nerves from each ganglion innervates the muscles within the leech body wall. The three muscle layers of the hydroskeleton (the circular, oblique, and longitudinal layers) and the dorsoventral muscles are responsible for the simple repertoire of behaviors.
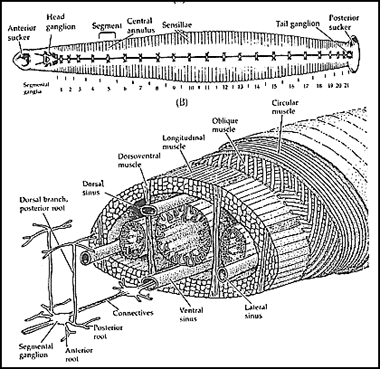
Medicinal leech anatomy.
Each ganglion contains at least 7 interneurons which can independantly sustain swim oscillations and are considered part of a swim segmental oscillator. These oscillator interneurons receive tonic excitatory drive (from segmental swimming interneurons) and fire with a triphasic rhythm due to a pattern of connectivity known as cyclic inhibition. These three phases of actvity center around 0, 120, and 240 degrees (see figure below) and provide both excitatory and inhibitory drive to motoneurons.
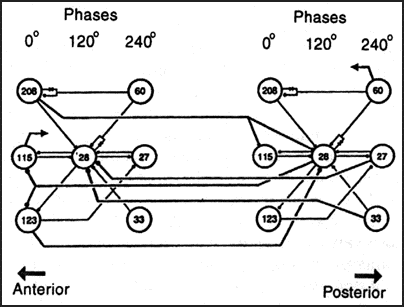
Circuit responsible for swimming in the medicinal leech. Oscillator interneurons are grouped into columns according to activity phase. Numbers refer to pairs of segmental interneurons (save for cell 208 which is unpaired). Cells 208, 115, and 123 project caudally while the remaineder project rostrally. All connections are inhibitory except those represented by diodes.
Although the segmental oscillatory interneurons fire in a triphasic rhythm, these neurons produce a four-phase rhythm in segmental body wall motoneurons. Each of these four classes of motoneurons fire for ~25% of the cycle. These classes consist of dorsal and ventral excitatory as well as inhibitory motoneurons. Intersegmental delays in motor activity are thought to be due to interganglionic connections. It appears that oscillator interneurons project to both anterior and posterior ganglia with some processes extending for at least five segments. These interganglionic connections are thought to provide coordination between segmental oscillators.
Anatomy drawing from Blackshaw and Nichols (1995). Circuit modified from Marder and Calabrese (1996).
SELECTED LEECH LINKS
Pictures and Classification of leeches
A great neuroscience search engine!
SELECTED REFERENCES
Early Classics:
Kuffler SW and Potter DD (1964). Glia in the leech nervous system: phjysiological properties and neuron-glia relationships. Journal of Neurophysiology 27: 290-320.
Muller KJ, Nicholls JG, & Stent GS (Eds.) (1981). Neurobiology of the Leech. Cold Spring Harbor publications, Cold Spring harbor, NY.
von Holst E (1973). The Behavioral Physiology of Animals and Man: Selected Papers. Vol. I. University of Miami Press, Coral Bables, Florida.
Reviews:
Brodfuehrer PD, Debski EA, O'Gara BA, and Friesen WO (1995). Neuronal control of leech swimming. Journal of Neurobiology 27: 403-418.
Camhi J (1984). Neuroethology: Nerve Cells and the Natural Behavior of Animals. Sinduer Associates, Sunderland, Mass.
Marder E and Calabrese RL (1996). Principles of rhythmic motor pattern generation. Physiological Reviews 76: 687-717.
Some Recent Advances:
Blackshaw SE and Nicholls JG (1996). Neurobiology and development of the leech. Journal of Neurobiology 27: 267-276.
Brodfuehrer PD and Burns A (1995). Neuronal factors influencing the decision to swim in the medicinal leech. Neurobiology of Learning and Memory 63: 192-199.
Brodfuehrer PD, Parker HJ, Burns A, and Berg M (1995). Regulation of the segmental swim-generating system by a pair of identified interneurons in the leech head ganglion. Journal of Neurophysiology 73: 983-992.
O'gara BA and Friesen WO (1995). Termination of leech swimming activity by a previously identified swim trigger neuron. Journal of Comparative Physiology A 177: 627-636.
This page prepared by:
Andrew Tate, Dec. 96
